Stacks and queues
Stacks and queues are dynamic sets in which the element removed from the set by the delete operation is prespecified. In a stack, the element deleted from the set is the one most recently inserted (LIFO policy). Similarly, in a queue, the element deleted is always the one that has been in the set for the longest time (FIFO policy).
Stack
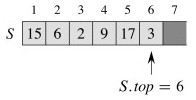
STACK-EMPTY(S) if S.top == 0 return TRUE else return FALSE
PUSH(S,x) S.top = S.top + 1 S[S.top] = x
POP(S) if STACK-EMPTY(S) error "underflow" eles S.top = S.top - 1 return S[S.top + 1]
Queues
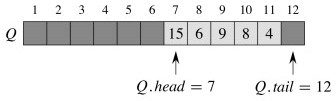
ENQUEUE(Q,x) Q[Q.tail] = x if Q.tail == Q.length Q.tail = 1 else Q.tail = Q.tail + 1
DEQUEUE(Q) x = Q[Q.head] if Q.head == Q.length Q.head = 1 else Q.head = Q.head + 1 return x
Notice: No error checking included.
Linked lists
A linked list is a data structure in which the objects are arranged in a linear order. Unlike an array, however, in which the linear order is determined by the array indices, the order in a linked list is determined by a pointer in each object. The data structure provides a simple, flexible representation for dynamic sets, supporting (though not necessarily efficiently) all the basic operations. A doubly linked list provides an extra pointer to the previous element.
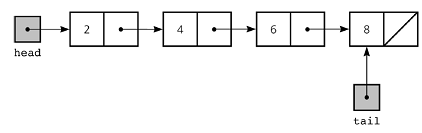
LIST-SEARCH(L,k) x = L.head while x != NIL and x.key != k x = x.next return x
LIST-INSERT(L,x) x.next = L.head if L.head != NIL L.head.prev = x L.head = x x.prev = NIL
LIST-DELETE(L,x) if x.prev != NIL x.prev.next = x.next else L.head = x.next if x.next != NIL x.next.prev = x.prev
Binary Trees
The methods for representing lists given in the previous section extend to any homogeneous data structure. In this section, we look specifically at the problem of representing rooted trees by linked data structures.
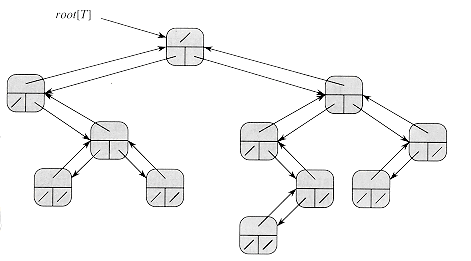
Each node stores pointers to parent, left child and right child. If x.p = NIL, then x is the root. If node x has no left child, then x.left = NIL, and similarly for the right child.
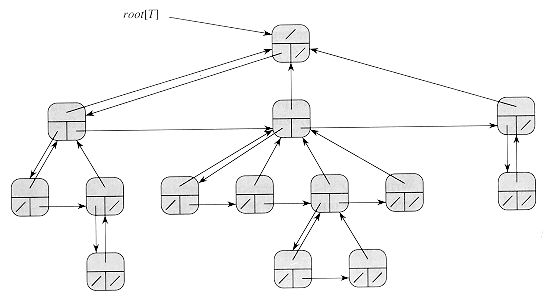
We can extend the scheme for representing a binary tree to any class of trees in which the number of children of each node is at most some constant k: we replace the left and right attributes by child1, child2, …, childk. The following scheme represents trees with arbitrary number of children. It has the advantage of using only O(n) space for any n-node rooted tree. The left-child, right-sibling representation contains a parent pointer p, and T.root points to the root of tree T. Instead of having a pointer to each of its children, however, each node x has only two pointers:
If node x has no children, then x.left-child = NIL, and if node x is the rightmost child of its parent, then x.right-sibling = NIL.