Hash Tables
A hash table is an effective data structure for implementing dictionaries. Although searching for an element in a hash table can take as long as searching for an element in a linked list - Θ(n) time in the worst case - in practice, hashing performs extremely well. Under reasonable assumptions, the average time to search for an element in a has table is O(1).
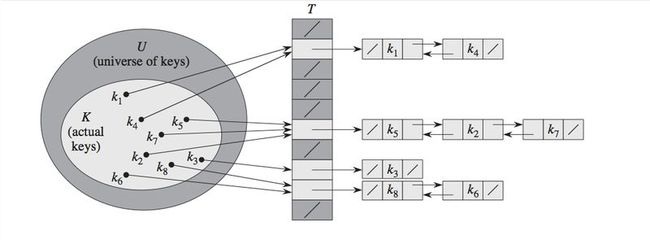
Imagine you have an empty array T of size n. You are given a key and some data you would like to store. You would use a hash function h to compute the slot from your key k into array T. In the figure above you see that the k1 maps to the second slot of the array T. However, what should we do if multiple values map to the same slot (produce the same key)? We call this situation a collision. The simplest resolution would be to make each slot contain a linked list and store the data consequently (also called chaining). An alternative method for resolving collisions is called open addressing, when all elements occupy the hash table itself. That is, each table entry contains either an element of the dynamic set or NIL. The advantage is that the latter avoids pointers all together. On the other hand, such hash table can “fill up” so that no further insertions can be made.
Hash Functions
Most hash functions assume that the universe of keys is the set of natural numbers. Thus, if the keys are not natural numbers, we find a way to interpret them as natural numbers. For example, we can interpret a character string as an integer expressed in suitable radix notation. Let’s look at some of the well-known methods:
The division method
In the division method for creating hash functions, we map a key k into one of the m slots by taking the remainder of k divided by m. That is, the hash function is
h(k) = k mod m.
[For example, m = 12, k = 100, h(k) = 4]
Since it requires only a single division operation, hashing by division is quite fast. When using the division method, we usually avoid certain values of m. For example, m should not be a power of 2, since if m = 2p, then h(k) is just the p lowest-order bits of k. A prime not too close to an exact power of 2 is often a good choice for m.
For example, suppose we wish to allocate a hash table, with collisions resolved by chaining, to hold roughly n = 2000 character strings, where a character has 8 bits. We don’t mind examining an average of 3 elements in an unsuccessful search, and so we allocate a hash table for size m = 701. We could choose m = 701 because it is a prime near 2000/3 but not near any power of 2. Treating each key k as an integer, our hash function would be h(k) = k mod 701.
The multiplication method
The multiplication method for creating hash functions operates in two steps. First, we multiply the key k by a constant A in the range 0 < A < 1 and extract the fractional part of kA. Then, we multiply this value by m and take the floor of the result. In short, the hash function is
h(k) = floor(m(kA mod 1)),
where kA mod 1 means the fractional part of kA, that is, kA - floor(kA). An advantage of this method is that the value of m is not critical. However, with some values it works better. The optimal choice depends on the characteristics of the data being hashed. One suggested value if A = (sqrt(5)-1)/2 = 0.6180339887…
Twitter Facebook Google+