ITA Baranov’s Walkthrough. Chapter 3

Growth of Functions

The order of growth of the running time of an algorithm gives a simple characterization of the algorithm’s efficiency and allows us to compare the relative performance of alternative algorithms. When we look at input sizes large enough to make only the order of growth of the running time relevant, we care about asymptotic efficiency of algorithms. That is, how it increases with the size of the input in the limit, as the size of the input increases without bound.

There are various kinds and flavors of asymptotic notations but these three are the ones you should definitely be familiar with:

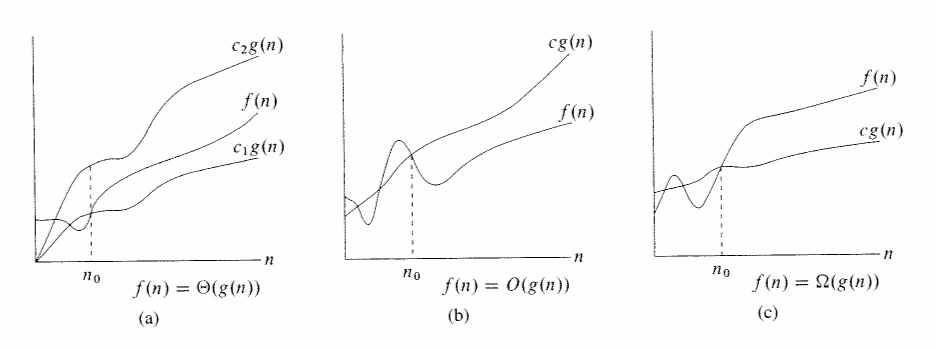
Θ(Big-theta) notation

For a given function g(n), we denote by Θ(g(n)) the set of functions such that some other function f(n) belongs to if there exist positive constants c₁ and c₂ such that it can be sandwiched between c₁g(n) and c₂g(n), for sufficiently large n. We say that g(n) is an asymptotically tight bound for f(n) since it bounds it from above and below.

O(Big-oh) notation

“Big-oh” provides us with only an asymptotic upper bound of the function. For a given function g(n), we denote by O(g(n)) the set of functions such that some other function f(n) belongs to if there exists positive constants c and n₀ such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n₀. That is, for all values n at and to the right of n₀, the value of the function f(n) is on or below cg(n).

Using this notation, we can often describe the running time of an algorithm merely by inspecting the algorithm’s overall structure. For example, the doubly nested loop structure of insertion sort yields an O(n²) upper bound on the worst-case running time. When we say “the running time is O(n²)”, we mean that there is a function f(n) that is O(n²) such that for any value of n, no matter what particular input of size n is chose, the running time on that input is bounded from above by the value f(n). In other words, it won’t run any slower than O(g(n)).

Ω(Big-omega) notation

Just as Ω-notation provides an asymptotic upper bound on a function, “Big-omega of g of n” provides an asymptotic lower bound. For a given function g(n), we denote by O(g(n)) the set of functions such that some other function f(n) belongs to if there exists positive constants c and n₀ such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n₀;

When we say that the running time of an algorithm is Ω(g(n)), we mean that no matter what particular input of size n is chosen for each value of n, the running time on that input is at least a constant * g(n), for sufficiently large n. In other words, it won’t run any faster than Ω(g(n)).

It’s important to note that running time of insertion sort belongs both to Ω(n) and O(n²) since it falls anywhere between a linear function of n and a quadratic function of n. Moreover, these bounds are asymptotically tight: for instance, the runnning time of insertion sort is not Ω(n^2), since there exists an input for which it runs in Θ(n) time (already sorted input). It is not contradictory, however, to say that the worst-case running time of insertion sort is Ω(n^2), since there exists such an input. From here it’s not hard to deduce that Θ-notation implies both “Big-oh” and “Big-omega” notations.

The rest of the chapter deals with some special cases and a bunch of math rules about logs/exponentials, things that are useful to know but can be easily looked up when needed.

Twitter Facebook Google+