Heaps
In this chapter, the book introduces another sorting algorithm: heapsort. Like merge sort, but unlike insertion sort, heapsort’s running time is O(nlgn). Like insertion sort, but unlike merge sort, heapsort sorts in place: only a constant number of array elements are stored outside the input array at any time. Thus, heapsort combines the better attributes of the two sorting algorithms we have already seen. It also introduces another algorithm design technique: using a data structure, in this case one called “heap” to manage information. Not only is the heap data structure useful for heapsort, but it also makes an efficient priority queue.
The (binary) heap data structure is an array object that we can view as a nearly complete binary tree. Each node of the tree corresponds to an element of the array. The tree is completely filled on all levels except possibly the lowest, which is filled from the left up to a point. An array A that represents a heap is an object with two attributes: A.length, which gives the number of elements in the array, and A.heap-size, which represents how many elements in the heap are stored within array A. The root of the tree is A[1], and given the index i of a node, we can easily compute the indices of its parent, left child, and right child:
PARENT(i) return floor(i/2)
LEFT(i) return 2i
RIGHT(i) return 2i+1
There are two kinds of binary heaps: max-heaps and min-heaps. In both kinds, the values in the nodes satisfy a heap property, the specifics of which depend on the kind of heap. In a max-heap: A[Parent(i)] >= A[i]. A min-heap is organized in the opposite way: A[Parent(i)] <= A[i].
Viewing a heap as a tree, we define the height of a node in a heap to be the number of edges on the longest simple downward path from the node to a leaf, and we define the height of the heap to be the height of its root. Since a heap of n elements is based on a complete binary tree, its height is Θ(lgn). Since the basic operations on heaps run in time at most proportional to the height of the tree, they take O(lgn) time.
Maintaining the heap property
In order to maintain the max-heap property, we call the procedure MAX-HEAPIFY. Its inputs are an array A and an index i into the array. When it is called, MAX-HEAPIFY assumes that the binary trees rooted as LEFT(i) and RIGHT(i) are max-heaps, but that A[i] might be smaller than its children, thus violating the max-heap property. The function lets the value at A[i] “go down” in the max-heap so that the subtree rotted at index i obeys the max-heap property.
MAX-HEAPIFY(A,i) l = LEFT(i) r = RIGHT(i) if l <= A.heap-size and A[l] > A[i] largest = l else largest = i if r <= A.heap-size and A[r] > A[largest] largest = r if largest != i exchange A[i] with A[largest] MAX-HEAPIFY(A,largest)
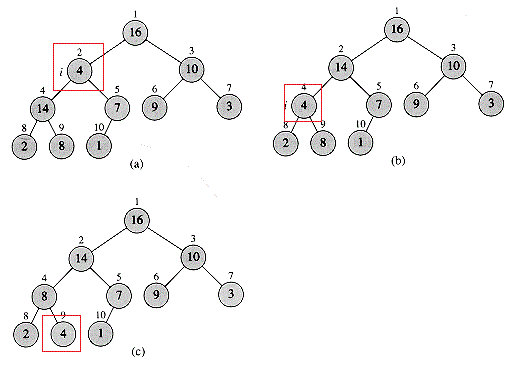
At each step, the largest of the elements A[i], A[LEFT(i)], and A[RIGHT(i)] is determined, and its index is stored in largest. If A[i] is largest, then the subtree rotted at node i is already a max-heap and the procedure terminates. Otherwise, one of the two children has the largest element, and A[i] is swapped with A[largest], which causes node i and its children to satisfy the max-heap property. The node indexed by largest, however, now has the original value A[i], and thus the subtree rooted as largest might violate the max-heap property. We call MAX-HEAPIFY recursively on that subtree. The running time can be described by the following recurrence: T(n) <= T(2n/3) + Θ(1). Using the master theorem, we conclude that T(n) = O(lgn) (case 2).
Building a heap
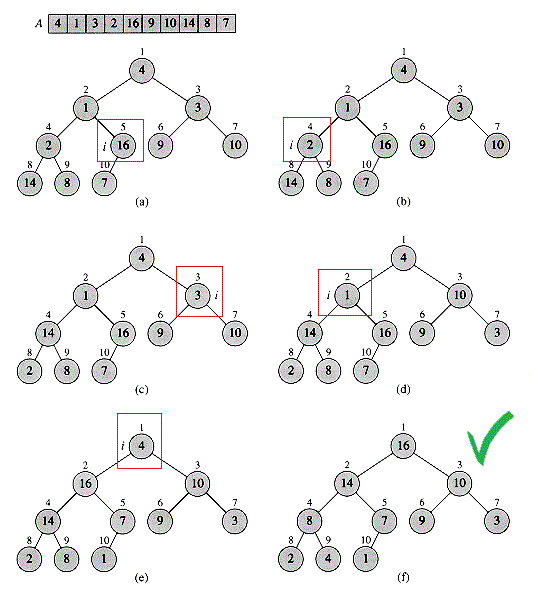
We can use the procedure MAX-HEAPIFY in a bottom-up manner to convert an array A[1..n], where n = A.length, into a max-heap. The elements in the subarray A[(floor(n/2)+1)..n] are all leaves of the tree, so each is a 1-element heap to begin with. The procedure BUILD-MAX-HEAP goes through the remaining nodes of the tree and runs MAX-HEAPIFY on each one. At first glance, the algorithm takes O(nlgn) since we do n iterations and each call to MAX-HEAPIFY takes O(lgn). However, a tighter bound will be O(n) since the time for MAX-HEAPIFY to run at a node varies with the height of the node in the tree, and the heights of most nodes are small.
BUILD-MAX-HEAP(A) A.heap-size = A.length for i = floor(A.length/2) downto 1 MAX-HEAPIFY(A,i)
The heapsort algorithm
The heapsort algorithm starts by using BUILD-MAX-HEAP to build a max-heap on the input array A[1..n], where n = A.length. Since the maximum element of the array is stored at the root A[1], we can put it into its correct final position by exchanging it with A[n]. If we now discard node n from the heap - and can do so by simply decrementing A.heap-size - we observe that the children of the root remain max-heaps, but the new root element might violate the max-heap property. All we need to do to restore the max-heap property, however, is call MAX-HEAPIFY(A,1), which leaves a max-heap in A[1..n - 1]. The heapsort algorithm that repeats this process for the max-heap of size n -1 down to a heap of size 2.
HEAPSORT(A) BUILD-MAX-HEAP(A) for i = A.length downto 2 exchange A[1] with A[i] A.heap-size = A.heap-size - 1 MAX-HEAPIFY(A,1)
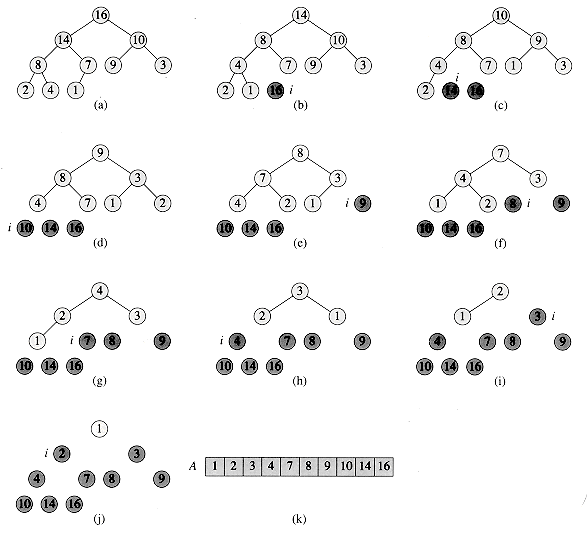
The HEAPSORT procedure takes time O(nlgn), since the call to BUILD-MAX-HEAP takes time O(n) and each of the n - 1 calls to MAX-HEAPIFY takes time O(lgn).